evaluating the business value of predictive models in python and r
By Jurriaan Nagelkerke, Data Science Consultant, and Pieter Marcus, Data Scientist
Why ROC curves are a bad idea to explain your model to business people
Summary
In this blog we explain four most valuable evaluation plots to assess the business value of a predictive model. These plots are cumulative gains, cumulative lift, response and cumulative response. Since these visualisations are not included in most popular model building packages or modules in R and Python, we show how you can easily create these plots for your own predictive models with our modelplotpy python module and our modelplotr R package (Prefer R? Read all about modelplotr here!). This will help you to explain your model’s business value in laymans terms to non-techies.
Intro

‘…And as we can see clearly on this ROC plot, the sensitivity of the model at the value of 0.2 on one minus the specificity is quite high! Right?…’.
If your fellow business colleagues didn’t already wander away during your presentation about your fantastic predictive model, it will definitely push them over the edge when you start talking like this. Why? Because the ROC curve is not easy to quickly explain and also difficult to translate into answers on the business questions your spectators have. And these business questions were the reason you’ve built a model in the first place!
What business questions? We build all kinds of supervised classification problems. Such as predictive models to select the best records in a dataset, which can be customers, leads, items, events… For instance: You want to know which of your active customers have the highest probability to churn; you need to select those prospects that are most likely to respond to an offer; you have to identify transactions that have a high risk to be fraudulent. During your presentation, your audience is therefore mainly focused on answering questions like Does your model enable us to our target audience? How much better are we, using your model? What will the expected response on our campaign be?
During our model building efforts, we should already be focused on verifying how well the model performs. Often, we do so by training the model parameters on a selection or subset of records and test the performance on a holdout set or external validation set. We look at a set of performance measures like the ROC curve and the AUC value. These plots and statistics are very helpful to check during model building and optimization whether your model is under- or overfitting and what set of parameters performs best on test data. However, these statistics are not that valuable in assessing the business value the model you developed.
One reason that the ROC curve is not that useful in explaining the business value of your model, is because it’s quite hard to explain the interpretation of ‘area under the curve’, ‘specificity’ or ‘sensitivity’ to business people. Another important reason that these statistics and plots are useless in your business meetings is that they don’t help in determining how to apply your predictive model: What percentage of records should we select based on the model? Should we select only the best 10% of cases? Or should we stop at 30%? Or go on until we have selected 70%?… This is something you want to decide togetherwith your business colleague to best match the business plans and campaign targets they have to meet. The four plots - cumulative gains, cumulative lift, response and cumulative response - we are about to introduce are in our view the best ones for that cause.
Get modelplotpy working on your machine
Let’s start this tutorial with installing the modelplotpy module. Modelplotpy is already available from Github, but currently it is not possible to install through the Python Package Index (PyPI) repository.
For some users we encountered that GitHub needs to be installed on your machine first. If you don’t have GitHub installed on your machine yet, it can be downloaded from here. After installing GitHub on your machine, it helps to restart and then continue with this tutorial.
Modelplotpy has to be installed through the command-line. On machines operating on macOS or Linux open the terminal and on Windows machines search for cmd.exe and hit enter. Copy and paste the command below and hit enter.
Once you have been able to install modelplotpy, it’s time to open Python and load it into the working directory and continue this tutorial! This tutorial has been written in Python 3.6.4 and may not work fully in Python 2.x.
Now we’re ready to use modelplotpy. In another post, we’ll go into much more detail on our modelplot packages in r and python and all its functionalities. Here, we’ll focus on using modelplotpy with a business example.
Example: Predictive models from sklearnon the Bank Marketing Data Set
Let’s get down to business! When we introduce the plots, we’ll show you how to use them with a business example. This example is based on a publicly available dataset, called the Bank Marketing Data Set. It is one of the most popular datasets which is made available on the UCI Machine Learning Repository. The data set comes from a Portugese bank and deals with a frequently-posed marketing question: whether a customer did or did not acquire a term deposit, a financial product. There are 4 datasets available and the bank-additional-full.csv is the one we use. It contains the information of 41.188 customers and 21 columns of information.
To illustrate how to use modelplotpy, let’s say that we work for this bank and our marketing colleagues have asked us to help to select the customers that are most likely to respond to a term deposit offer. For that purpose, we will develop a predictive model and create the plots to discuss the results with our marketing colleagues. Since we want to show you how to build the plots, not how to build a perfect model, we’ll use six of these columns in our example. Here’s a short description on the data we use:
y: has the client subscribed a term deposit? duration: last contact duration, in seconds (numeric) campaign: number of contacts performed during this campaign and for this client pdays: number of days that passed by after the client was last contacted from a previous campaign previous: number of contacts performed before this campaign and for this client (numeric) euribor3m: euribor 3 month rate
Let’s load the data and have a quick look at it:
On this data, we’ve applied some predictive modeling techniques from the sklearn module. This well known module is a wrapper for many predictive modeling techniques, such as logistic regression, random forest and many, many others. Lets train a few models to evaluate with our plots.
In another post, we’ll go into much more detail on our modelplot packages in R and Python and all its functionalities. For now, we focus on explaining to our marketing colleagues how good our predictive model can help them select customers for their term deposit campaign.
What just happened? In the modelplotpy a class is instantiated and the plotting_scope function specifies the scope of the plots you want to show. In general, there are 3 methods (functions) that can be applied to the modelplotpy class but you don’t have to specify them since they are chained to each other. These functions are:
prepare_scores_and_deciles: scores the customers in the train dataset and test dataset with their probability to acquire a term deposit aggregate_over_deciles: aggregates all scores to deciles and calculates the information to show plotting_scope. allows you to specify the scope of the analysis.
In the second line of code, we specified the scope of the analysis. We’ve not specified the “scope” parameter, therefore the default - no comparison - is chosen. As the output notes, you can use modelplotpy to evaluate your model(s) from several perspectives:
Interpret just one model (the default) Compare the model performance across different datasets Compare the performance across different models Compare the performance across different target classes
Here, we will keep it simple and evaluate - from a business perspective - how well a selected model will perform in a selected dataset for one target class. We did specify values for some parameters, to focus on the random forest model on the test data. The default value for the target class is term deposit ; since we want to focus on customers that do take term deposits, this default is perfect.
Let’s introduce the Gains, Lift and (cumulative) Response plots.
Before we throw more code and output at you, let’s get you familiar with the plots we so strongly advocate to use to assess a predictive model’s business value. Although each plot sheds light on the business value of your model from a different angle, they all use the same data:
Predicted probability for the target class Equally sized groups based on this predicted probability Actual number of observed target class observations in these groups
It’s common practice to split the data to score into 10 equally large groups and call these groups deciles. Observations that belong to the top-10% with highest model probability in a set, are in decile 1 of that set; the next group of 10% with high model probability are decile 2 and finally the 10% observations with the lowest model probability on the target class belong to decile 10.
Each of our four plots places the deciles on the x axis and another measure on the y axis. The deciles are plotted from left to right so the observations with the highest model probability are on the left side of the plot. This results in plots like this:
Now that it’s clear what is on the horizontal axis of each of the plots, we can go into more detail on the metrics for each plot on the vertical axis. For each plot, we’ll start with a brief explanation what insight you gain with the plot from a business perspective. After that, we apply it to our banking data and show some neat features of modelplotpy to help you explain the value of your wonderful predictive models to others.
1. Cumulative gains plot
The cumulative gains plot - often named ‘gains plot’ - helps you answer the question:
When we apply the model and select the best X deciles, what % of the actual target class observations can we expect to target?
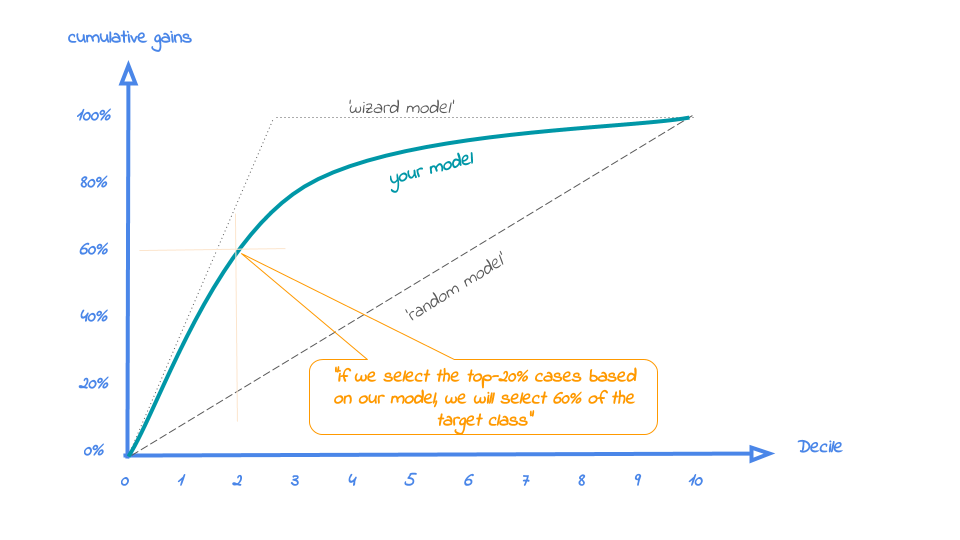
Hence, the cumulative gains plot visualises the percentage of the target class members you have selected if you would decide to select up until decile X. This is a very important business question, because in most cases, you want to use a predictive model to target a subset of observations - customers, prospects, cases,… - instead of targeting all cases. And since we won’t build perfect models all the time, we will miss some potential. And that’s perfectly all right, because if we are not willing to accept that, we should not use a model in the first place. Or build a perfect model, that scores all actual target class members with a 100% probability and all the cases that do not belong to the target class with a 0% probability. However, if you’re such a wizard, you don’t need these plots any way or you should have a careful look at your model - maybe you’re cheating?….
So, we’ll have to accept we will lose some. What percentage of the actual target class members you do select with your model at a given decile, that’s what the cumulative gains plot tells you. The plot comes with two reference lines to tell you how good/bad your model is doing: The random model line and the wizard model line. The random model line tells you what proportion of the actual target class you would expect to select when no model is used at all. This vertical line runs from the origin (with 0% of cases, you can only have 0% of the actual target class members) to the upper right corner (with 100% of the cases, you have 100% of the target class members). It’s the rock bottom of how your model can perform; are you close to this, then your model is not much better than a coin flip. The wizard model is the upper bound of what your model can do. It starts in the origin and rises as steep as possible towards 100%. If less than 10% of all cases belong to the target category, this means that it goes steep up from the origin to the value of decile 1 and cumulative gains of 100% and remains there for all other deciles as it is a cumulative measure. Your model will always move between these two reference lines - closer to a wizard is always better - and looks like this:
Back to our business example. How many of the term deposit buyers can we select with the top-20% of our predictive models? Let’s find out! To generate the cumulative gains plot, we can simply call the function plot_cumgains():

We only have to specify the input with the plotting_scope output. There are several parameters available to customize the plot, though. If we want to emphasize the model performance at a given point, we can add both highlighting to the plot and add some explanatory text below the plot. Both are optional, though:

Our ‘highlight_decile’ parameter adds some guiding elements to the plot at decile 2 as well as a text box below the graph with the interpretation of the plot at decile 2 in words. This interpretation is also printed to the console. Our simple model - only 6 pedictors were used - seems to do a nice job selecting the customers interested in buying term deposites. When we select 20% with the highest probability according to random forest, this selection holds 79% of all term deposit cases in test data. With a perfect model, we would have selected 100%, since less than 20% of all customers in the test set buy term deposits. A random pick would only hold 20% of the customers with term deposits. How much better than random we do, brings us to plot number 2!


