Evaluation of clustering
聚类的目标
high intra-cluster similarity and low inter-cluster similarity
数据集有groundtruth时,如何评估聚类结果的优劣?
4种评估方法
- purity。 简单。
- NMI。从信息论角度解释。
- RI。实质是accuracy,同时惩罚了FP和FN两种错误。
- F-measure。为不同的错误类型(FP和FN)赋予不同的权重。
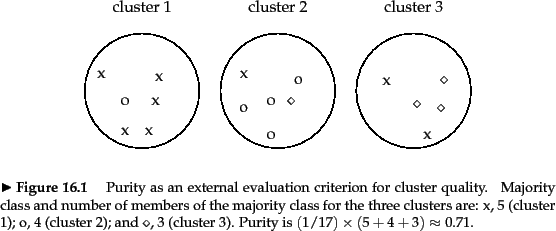
purity
purity取值范围[0,1],越大越好。 当cluster数量(k)很大时,purity值容易高,极端情况下,当一个类只包含一条记录时,purity取1.
begin{equation}
purity(W,C) = frac {1}{N} sum_k max_j |w_k cap c_j| label{rij}
end{equation}
N为数据集大小,$W=\{w_1,w_2,…,w_k\}$ is the set of clusters,即聚类结果。 $C = \{c_1,c_2,…,c_j\}$ is the set of classes,即groundtruth. 取$w_k$与$c_j$交集的最大值。
begin{equation}
purity(W,C) = frac {1}{17} *(5+4+3)approx 0.71
end{equation}
NMI
begin{equation}
NMI(W,C) = frac {I(W,C)}{[H(W)+H(C)]/2}
end{equation}
$I(W,C)$衡量类W与groundtruth C之间的互信息。
begin{align}
I(W,C) &= sum_k sum_j P(w_k cap c_j) log frac {P(w_k cap c_j)}{P(w_k)P(c_j)} nonumber \
&= sum_k sum_j frac{|w_k cap c_j| }{N} log frac {N|w_k cap c_j| }{|w_k||c_j|} label{imp}
end{align}
当类与groundtruth之间关系随机时,互信息取0。当类与groundtruth一样时,互信息取1,当类进一步分割成更小的类时,互信息不变。
极端情况下,当一个类只包含一条记录时,互信息仍然取1. 因此使用熵来惩罚过大的类数量。(熵随着类数目的增加而增加,极端情况下,当一个类只包含一条记录时,熵取最大值)
$H(W)$ 和$H(C)$分布衡量类W与groundtruth C的熵 (entropy).
begin{equation}
H(W) = - sum_k P(w_k) log P(w_k)
end{equation}
$P(w_k)$ 用 cluster $w_k$中的记录在总数据集的出现频率来估算,即$P(w_k)=|w_k|/N$
RI (Rand index)
| 类型 | 说明 |
|---|---|
| TP | 2个相似实体被分配到了相同类中 |
| TN | 2个不相似实体分配到了不同类中 |
| FP | 2个不相似实体分配到了相同类中 |
| FN | 2个相似实体分配到了不同类中 |
begin{equation}
RI(W,C) = frac {TP+TN}{TP+FP+FN+TN}
end{equation}
例子:
$TP+FP = C_6^2+C_6^2+C_5^2 = 40$
$TP = C_5^2+C_4^2+C_3^2+C_2^2 = 20$
thus $FP = 40 -20 = 20$
for each classes, $x:8,o:5,diamondsuit:4$
the number of similar entities: $TP+FN = C_8^2+C_5^2+C_4^2 = 44$
$FN = 44 - 20 = 24$
the number of dissimilar entities : $ TN+FP = 8times5+8times 4+5times4=92$
$TN = 92-20 = 72$
| same cluster | different clusters | |
|---|---|---|
| same class | TP=20 | FN=24 |
| different classes | FP=20 | TN=72 |
F-measure
$Precision = TP/(TP+FP)$
$Recall= TP/(TP+FN)$
$F_beta = frac{(beta^2+1)PR}{beta^2P+R}$
当$beta > 1$时,更多的权重给Recall,对FN的惩罚力度更强。


